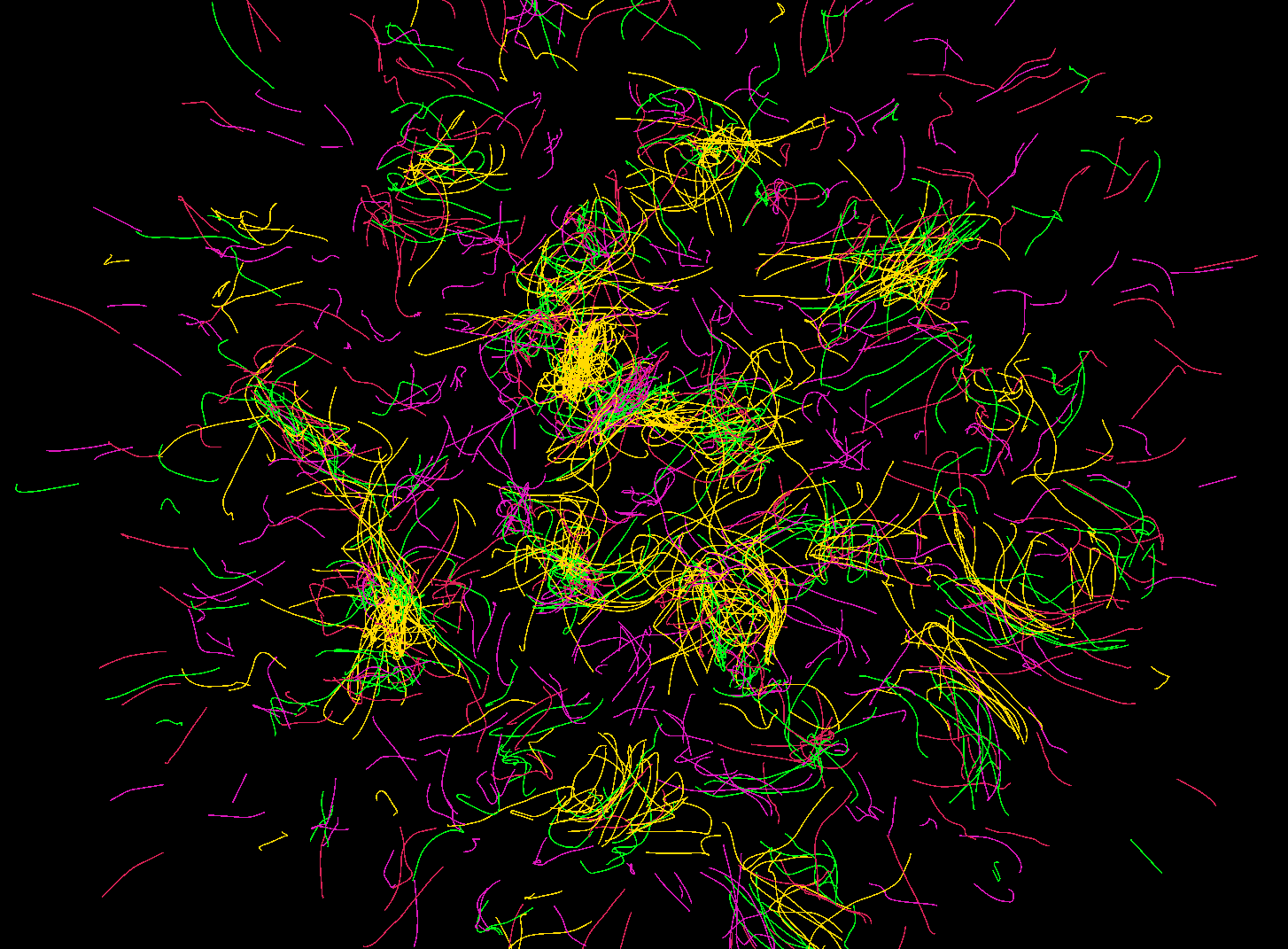
Simulator.cs doesn’t drive the scene with hand-authored animation or fancy shaders. It spawns four families of particles, A, B, C, and D, and lets the math of their pairwise attraction/repulsion rules decide what the frame looks like. Every frame recomputes those forces, so the visible motion is the sum of tiny decisions instead of a scripted path.
Particle families and setup
Each family owns numberOfParticles lightweight Particle instances with positions, velocities, and a max speed limit. They spawn inside a circle and receive randomized velocities before Unity instantiates a prefab for each one. The simulator also generates a unique AnimationCurve plus [minDist, maxDist] for every ordered pair (A->B, B->C, etc.), so every run uses a fresh rule set.
void Start()
{
// allocate particles/transforms per family
ParticlesA = new Particle[numberOfParticles];
ParticlesB = new Particle[numberOfParticles];
ParticlesC = new Particle[numberOfParticles];
ParticlesD = new Particle[numberOfParticles];
TransformsA = new Transform[numberOfParticles];
TransformsB = new Transform[numberOfParticles];
TransformsC = new Transform[numberOfParticles];
TransformsD = new Transform[numberOfParticles];
// spawn each family with random position/velocity, then instantiate
for (int j = 0; j < numberOfParticles; j++)
{
ParticlesA[j] = new Particle(RandomPosition(), RandomVelosity(), VelosityMax);
ParticlesB[j] = new Particle(RandomPosition(), RandomVelosity(), VelosityMax);
ParticlesC[j] = new Particle(RandomPosition(), RandomVelosity(), VelosityMax);
ParticlesD[j] = new Particle(RandomPosition(), RandomVelosity(), VelosityMax);
TransformsA[j] = Instantiate(particlePrefabA, ParticlesA[j].position, Quaternion.identity, null).transform;
TransformsB[j] = Instantiate(particlePrefabB, ParticlesB[j].position, Quaternion.identity, null).transform;
TransformsC[j] = Instantiate(particlePrefabC, ParticlesC[j].position, Quaternion.identity, null).transform;
TransformsD[j] = Instantiate(particlePrefabD, ParticlesD[j].position, Quaternion.identity, null).transform;
}
}How it works
- Each frame recomputes the force on every particle by summing contributions from the other three families. GetForceA/GetForceB/… just call the shared CalculateForce helper with the corresponding SpatialGrid, Particle[], and InteractionConfig.
- CalculateForce only visits nearby particles by hashing them into a grid whose cell size matches the longest interaction radius. It loops over neighboring cells up to cellRadius, so it never misses an influencer without scanning the whole population.
- Only distances within [minDist², maxDist²] participate. The code normalizes the true distance to [0, 1] via (distance – minDist) / (maxDist – minDist) and samples the cached AnimationCurve, multiplying the scalar by forceScaler and the normalized displacement direction.
- Every computed force is scaled by Time.deltaTime, passed to Particle.ApplyForce, and then the particle’s position is updated and bounded (the current Wrap is a no-op, so the bounds are more aspirational for now).
Private Vector2 CalculateForce(Particle source, SpatialGrid grid, Particle[] targets, InteractionConfig config)
if (source == null || grid == null || targets == null || config.maxDist <= config.minDist)
return Vector2.zero;
grid.GetCell(source.position, out int x, out int y);
Vector2 force = Vector2.zero;
for (int offsetX = -config.cellRadius; offsetX <= config.cellRadius; offsetX++)
{
for (int offsetY = -config.cellRadius; offsetY <= config.cellRadius; offsetY++)
{
if (!grid.TryGetCell(x + offsetX, y + offsetY, out var cell))
continue;
foreach (int targetIndex in cell)
{
Vector2 displacement = source.position - targets[targetIndex].position;
float distanceSquared = displacement.sqrMagnitude;
if (distanceSquared < config.minDistSq || distanceSquared > config.maxDistSq)
continue;
float distance = Mathf.Sqrt(distanceSquared);
if (distance < 0.0001f)
continue;
float normalized = config.inverseRange > 0f ? (distance - config.minDist) * config.inverseRange : 0f;
float curveValue = config.sampler.Evaluate(normalized);
force += (displacement / distance) * (curveValue * forceScaler);
}
}
}
return force;
}Why you see those patterns

Why you see those patterns
Every ordered pair (A->B, B->A, etc.) contributes a term to a coupled-looking differential system:
F₁ = Σ ((source − target).normalized × curve((|d| − min)/range) × forceScaler)
The direction comes from the normalized displacement, while the magnitude comes from whatever curve you provided, positive values attract, negative repel. Smooth curves produce soft clustering; sharp peaks trigger energetic oscillations and shells. Opposing curves create orbiting equilibria around their zero crossings. Because all curves and ranges are randomized on startup, the system behaves like a live experiment in emergent particle art every time.
What to expect
Visual output varies run-to-run, but common motifs are:
- Swirling filaments where one family chases another.
- Drifting, layered shells where attraction balances repulsion.
- Momentary clumps that form, burst, and reform as the curves fluctuate.
The damping parameter keeps the kinetic energy in check, and the spatial grid keeps the update loop fast even with thousands of particles.